Unlock the secrets of the Floyd Warshall Algorithm with this comprehensive step-by-step guide for mastering dynamic programming techniques!

Hey there, fellow algorithm enthusiasts! Today, we’re diving into the fascinating world of the Floyd Warshall Algorithm. This powerful algorithm is a key player in the realm of graph theory, particularly when it comes to finding the shortest paths between all pairs of vertices in a graph. So, grab a cup of coffee and let’s explore the Floyd Warshall Algorithm together!

Understanding the Floyd Warshall Algorithm

At its core, the Floyd Warshall Algorithm is all about dynamic programming and memoization. The goal is to efficiently calculate the shortest paths between all pairs of vertices in a graph. By leveraging the concept of memoization, the algorithm avoids redundant calculations and optimizes the process of finding the shortest paths.

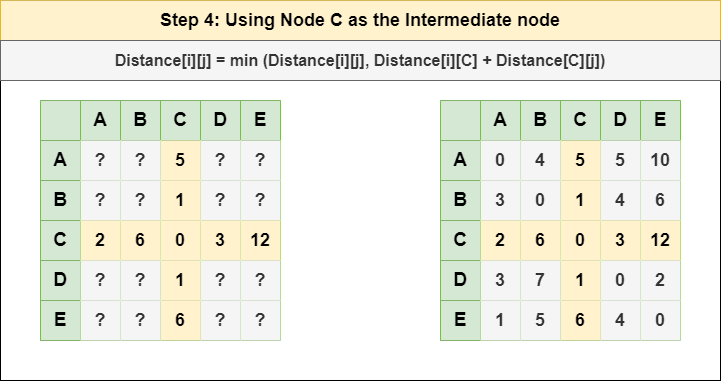
The key steps involved in implementing the Floyd Warshall Algorithm can be broken down into a few main components. First, we initialize a matrix to store the distances between all pairs of vertices. Then, we iterate through each vertex and update the distance matrix based on the shortest paths found so far. This process continues until all vertices have been considered, resulting in a final distance matrix that contains the shortest paths between all pairs of vertices.

Real-World Example: Finding the Shortest Paths in a Transportation Network

Imagine we have a transportation network with multiple cities connected by roads. Our goal is to determine the shortest paths between all pairs of cities using the Floyd Warshall Algorithm. Let’s walk through a step-by-step example to see how the algorithm works in action.

First, we initialize a distance matrix that represents the distances between the cities in our transportation network. We then iterate through each city and update the distance matrix based on the shortest paths found so far. As the algorithm progresses, the distance matrix is continually refined to reflect the shortest paths between all pairs of cities.

Benefits and Limitations of the Floyd Warshall Algorithm

The Floyd Warshall Algorithm offers a range of benefits when it comes to solving the all-pairs shortest path problem. One of the key advantages is its efficiency in finding the shortest paths between all pairs of vertices in a graph. By leveraging dynamic programming and memoization, the algorithm minimizes redundant calculations and optimizes the process of determining the shortest paths.

 

However, it’s important to consider the limitations of the Floyd Warshall Algorithm, particularly when dealing with large-scale networks. As the size of the graph increases, the algorithm’s time complexity can become a challenge, affecting its practicality for certain applications. It’s crucial to weigh the benefits and limitations of the algorithm when deciding whether to apply it to a specific problem.

Conclusion

In conclusion, the Floyd Warshall Algorithm is a powerful tool for finding the shortest paths between all pairs of vertices in a graph. By leveraging dynamic programming and memoization, the algorithm efficiently calculates the shortest paths and optimizes the process of solving the all-pairs shortest path problem. Whether you’re exploring graph theory or tackling real-world optimization challenges, the Floyd Warshall Algorithm is a valuable addition to your algorithmic toolkit. So, roll up your sleeves and start mastering the Floyd Warshall Algorithm today!